 | 메모장_물리 | |
|
@ 2004-11-23 @
1 하드웨어 가속 ##.PPU(물리연산 프로세스 유닛) ; CPU가 담당하는 이미지 재생과 관련된 물리 연산을 전담하는 주변기기
/ 콘솔 게임프로세싱 처리 개념 = CPU + GPU + PPU
#.GPU (Graphics Processing Unit)는중앙처리장치인 CPU만으로 고정밀도의 그래픽을 단독으로 처리하기에 무리가 있기 때문에, 이를 보조하기 위하여 3D그래픽 연산 전용의 프로세서 GPU가 개발 되었습니다.
GPU라는 용어는 엔비디아(NVIDIA)사에서 1999년에 ‘지포스(GeForce)’라는 이름의 새로운 그래픽 컨트롤러(Graphics Controller: 그래픽카드용 칩)을 내놓으며 처음 제창한 것이다. 지포스는 CPU의 도움 없이 자체적으로 폴리곤(Polygon: 3D 그래픽을 구성하는 도형)의 변형(Transform) 및 광원(Lighting)효과를 구사하는 기능, 이른바 ‘하드웨어(Hardware) T&L’을 갖추고 있었다. 이는 이전까지 사용했던 그래픽 컨트롤러와는 확연히 다른 개념이었기 때문에 이를 구분하고자 GPU라는 이름이 붙게 되었다. 그리고 지포스의 출시 후 1년이 지난 2000년, ATi(현재의 AMD)사에서 ‘라데온(Radeon)’이라는 GPU를 출시하게 되면서 양사의 경쟁이 본격화 된다.
#.인텔 > Havok - 물리 계산을 CPU에서 보조 역할을 담당
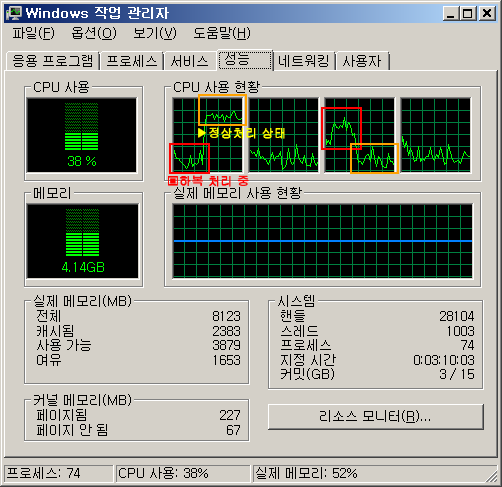
배경 설정이나 이펙트 등에 물리(하복) 연산이 진행될 때, 다른 프로세스가 작동
#.NVIDIA > (AGEIA) PhysX - 물리 계산을 그래픽카드에서 보조 역할을 담당--> 심할 경우, 물리 계산이 끝날 때까지 화면이 멈추는 현상 발생 2 게임에서의 물리학 #
2.1 Euler's Method #
2.2 Hook's law #
2.3 Verlet Intergrator #
-2) 초기치 R(t-Δt) = R(t) - V(t)*Δt 로 계산
-3) 예상해던 결과가 나오면 2~3번 루프를 돌려서 해당 프레임에서 고정시킬 수 있다. 3 Chaos #
4 Jump 기본로직 #
const float JumpGHIGHTRAVITY 1800.0f
const float SAFEHEIGHT = 2.0f;
const float STARTJUMP = 100.0f;
static float fUp = 0.0f;
// 점프 여부
if( !점프중 && 현재 애니메이션이 점프인가? )
{
m_bJumpstart = true;
m_bJump = true;
fUp = STARTJUMP;
m_fGravity = 0.0f;
}
if( m_bJump ) // 상승 부분
{
m_fGravity += (JumpGHIGHTRAVITY * (fDelta*fDelta)*0.5f );
fUp -= m_fGravity;
if( fUp < 0.0f )
{
m_fGravity = 0.0f;
m_bJump = false;
}
else
{
oldTrans.z += fUp;
}
}
else // 낙하 여부
{
if( (oldTrans.z - kNewTrans.z) > SAFEHEIGHT )
{
m_fGravity += (JumpGHIGHTRAVITY * (fDelta*fDelta)*0.5f );
oldTrans.z -= m_fGravity;
}
else
{
oldTrans = kNewTrans;
m_fGravity = 0.0f;
m_bJumpstart = false;
}
}
class className
{
public:
void StartJump();
private:
Point3 m_vSavePosition;
bool m_bJump02; // 점프 이벤트를 받아서 캐릭터가 현재 상승 중인지를 표시
bool m_bJumpstart; // 점프를 할 수 있는 상태 인지를 표시
float m_fGravity;
float m_fHightPos;
float m_fJumpStartTime;
float m_fJumpTime;
float m_fJumpTimeMAX;
}
-----------------------------------------------------------------------------------
const float DEF_JumpGHIGHTRAVITY = 1600.0f;
const float DEF_JumpRAD = PI * 0.5; // 90도
const float DEF_JumpMAX = 12.0f; // jump시 최고 정점의 높이
void className::StartJump()
{
if( m_bJumpstart == true )
return;
CPlayer * pkPlayer = GetPlayer();
_TKASSERT( pkPlayer );
m_pSavePosition = pkPlayer->GetWorldTranslate();
ControllerSequence* pkSequence = pkPlayer->GetSequence(Animation_jump);
m_fJumpTimeMAX = pkSequence->GetLength() * 1.1f;
m_fJumpTime = m_fJumpTimeMAX * 0.5f;
m_fJumpStartTime = GetCurTime();
m_bJumpstart = true;
m_bJump02 = true;
}
bool className::UpDate()
{
...
// 점프 및 낙하 부분 - Sin곡선을 따라서 상승 후 정점에서 함수 사용해서 낙하
//=========================================================================================
float fjumptime = GetCurTime() - m_fJumpStartTime;
if( m_bJump02 ) // 점프시 상승 구간
{
float fjumpRAD = (fjumptime/m_fJumpTime) * DEF_JumpRAD;
if( fjumptime < m_fJumpTime ) // 상승 중
{
m_fHightPos = Sin(fjumpRAD) * DEF_JumpMAX;
m_fHightPos += m_vSavePosition.z;
}
else // 최고 정점부분
{
m_fHightPos = m_vSavePosition.z + DEF_JumpMAX;
m_bJump02 = false;
}
}
else //점프가 아닐때 낙하
{
if((oldTrans.z - kNewTrans.z) < 2.0f)
{
m_fHightPos = kNewTrans.z;
oldTrans = kNewTrans;
}
if(m_fHightPos > kNewTrans.z)
{
m_fGravity += (DEF_JumpGHIGHTRAVITY * ((fDelta*fDelta)*0.5));
m_fHightPos -= m_fGravity;
}
else // if(m_fHightPos <= kNewTrans.z)
{
m_fHightPos = kNewTrans.z;
m_fGravity = 0.0f;
m_bJumpstart = false;
m_bJump02 = false;
}
}
oldTrans.z = m_fHightPos;
}
|
"호랑이는 가죽 땜시 디지고, 사람은 이름 땜시 디지는 거여!" 메모장_소프트웨어3D edu2014 HelpOnNavigation 메모장_감사의길 |
